MODULE 1: Numbers to 10
Kindergarten students start out solidifying the meaning of numbers to 10 with a focus on number values and relationships using fingers, cubes, drawings, 5 groups and the Rekenrek. Students then investigate patterns of "1 more" and "1 less". Because fluency with addition and subtraction within 5 is a Kindergarten goal, addition within 5 is introduced in Module 1.
KEY CONCEPTS:
*Exactly the same/not exactly the same/ the same but ...
*Sort - group objects according to a particular attribute (ex. color, shape and size)
*Counting "how many" in a set or given group arranged in a linear, array, circular or scattered configuration as shown below:
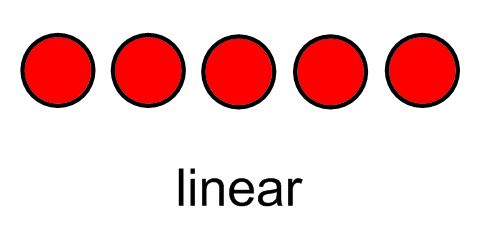
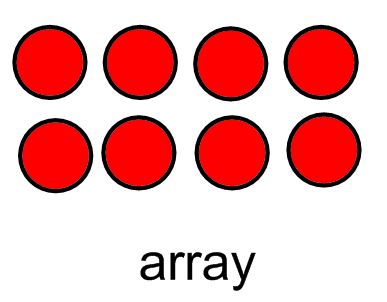
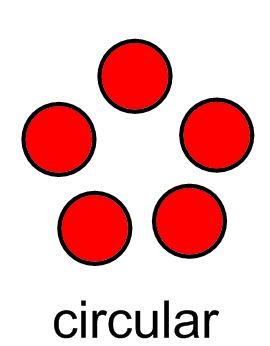
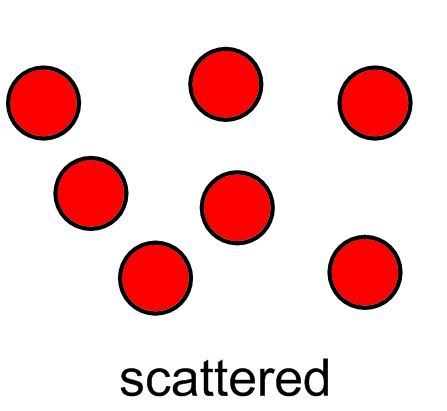
KEY CONCEPTS:
*Exactly the same/not exactly the same/ the same but ...
*Sort - group objects according to a particular attribute (ex. color, shape and size)
*Counting "how many" in a set or given group arranged in a linear, array, circular or scattered configuration as shown below:
*Finding "hidden partners"
Example breaking down 5 into two groups: 3 and 2
3 and 2 are the hidden partners
*Number sentence (3=2+1)
* 5 group
*1 more (one more than 4 is 5)
*1 less (one less than 4 is 3)
TOOLS USED:
Number path 1-10: a pictorial representation of numbers and number order. Each space is a visual representation of one number, one space, and each number being equal in size. The color change at 5 helps to reinforce the the concepts of 5 and 10.

Rekenenrek: A Rekenrek is simpy a counting tool with beads like an abacus. The Rekenrek has a 5 and 10 structure with a color change at 5. The 20 bead Rekenrek consists of 2 rows of 10 beads, allowing students to see numbers to 10 as a number line in one row or a ten-frame (5 beads on two rows)

Ten-Frame: A ten-frame is a 2 by 5 grid (array) used to develop understandings of concepts such as 5 patterns and combinations of numbers to 10.

Example breaking down 5 into two groups: 3 and 2
3 and 2 are the hidden partners
*Number sentence (3=2+1)
* 5 group
*1 more (one more than 4 is 5)
*1 less (one less than 4 is 3)
TOOLS USED:
Number path 1-10: a pictorial representation of numbers and number order. Each space is a visual representation of one number, one space, and each number being equal in size. The color change at 5 helps to reinforce the the concepts of 5 and 10.
Rekenenrek: A Rekenrek is simpy a counting tool with beads like an abacus. The Rekenrek has a 5 and 10 structure with a color change at 5. The 20 bead Rekenrek consists of 2 rows of 10 beads, allowing students to see numbers to 10 as a number line in one row or a ten-frame (5 beads on two rows)
Ten-Frame: A ten-frame is a 2 by 5 grid (array) used to develop understandings of concepts such as 5 patterns and combinations of numbers to 10.